Dificultades en el aprendizaje de operaciones con números enteros en educación media superior
- 1 de junio de 2024
- En palabras de Junio 2024
Difficulties in learning operations with whole numbers in high school
Dra. López Castañeda, Rosa María
Profra. de Matemáticas EPO 222
Dra. Rodríguez González, María Leticia
Profra. de doctorado CESE
Resumen
Esta investigación se realizó en la Preparatoria Oficial 222 (EPO 222), identificando las dificultades que presentan los estudiantes de primer semestre en el área de matemáticas, considerando las condiciones del regreso a las aulas por la contingencia sanitaria del COVID 19, que agudizó las dificultades de aprendizaje en todas las áreas curriculares; agravándose en las comunidades marginadas del país. Se diseñaron e implementaron distintas estrategias para trabajar en modelo hibrido: encontrando que no han logrado el aprendizaje de los números enteros, lo que les dificulta continuar con los siguientes contenidos como álgebra. La fundamentación teórica de los Modelos Teóricos Locales posibilitó el análisis de este estudio exploratorio, concluyendo con la necesidad de abrir una línea de investigación de esta problemática en Educación Media Superior (EMS), para diseñar estrategias eficaces de intervención didáctica.
Palabras clave: Dificultades, aprendizaje, números enteros, educación media superior
Abstract
This research was carried out in the Official High School 222 (EPO 222), identifying the difficulties presented by first-semester students in the area of mathematics, considering the conditions of the return to the classroom due to the health contingency of COVID 19, which exacerbated learning difficulties in all curricular areas, worsening in the country’s marginalized communities. Different strategies were designed and implemented to work in a hybrid model: finding that they have not achieved the learning of integers, which makes it difficult for them to continue with the following contents such as algebra. The theoretical foundation of the Local Theoretical Models made possible the analysis of this exploratory study, concluding with the need to open a line of research on this problem in this educational level (EMS), to design effective strategies of didactic intervention.
Key words: Difficulties, learning, whole numbers, high school
Problematización: Aprendizaje de los números enteros
La migración a entornos virtuales por el confinamiento al que fuimos obligados por el Covid-19, dificultó el desarrollo de los procesos de aprendizaje, pues el 6.6% de los estudiantes no tenían dispositivos digitales, ni guía escolar; del 7.8 millones de estudiantes que, si tuvieron un dispositivo electrónico, no contaron con apoyo personal que guiara su aprendizaje en casa (INEGI, 2020, citado en IMCO, 2021). A esto hay que agregar que no todos los alumnos contaron con los dispositivos, computadoras o Internet que les permitieran incorporarse a las clases virtuales, lo que generó una brecha digital qué puso al descubierto las desigualdades estructurales y profundizó el rezago en los aprendizajes de los estudiantes. Además, es importante destacar que no todos los estudiantes tenían acceso a dispositivos, computadoras o conexión a Internet, lo que exacerbó la brecha digital y agravó las desigualdades estructurales, resultando en un mayor rezago en el aprendizaje de los alumnos (Hevia y Vergara, 2021)
La EPO 222, está ubicada en Chimalhuacán, Edo. de México, reportada como zona marginada; donde la mayoría de los alumnos de nuevo ingreso no aprobaron el examen para ingresar a otras instituciones de Educación Media Superior (EMS). Para los alumnos de primer grado el tema de los números enteros constituyó un problema constante de reprobación. Hernández y Noriega (2017) consideran que “los principales errores detectados en Álgebra se deben a la deficiencia en las habilidades aritméticas de los alumnos, quienes encuentran muy complicado entender y expresarse en el lenguaje matemático” (p. 16). Para conceptualizar los números enteros, es necesario establecer la relación de números positivos y negativos. Sin embargo, Gallardo y Rojano (1987), afirman que a “los estudiantes les resulta complicado comprender y conceptualizar los negativos” (p. 9). Mientras que Maca (2016) describe que es común que los estudiantes de educación básica y Educación Media Superior responden que “no se puede” cuando se les pregunta cuál es el resultado de la operación 5 – 8. Por otra parte, Gallardo y Basurto (2010) demostraron que los estudiantes de educación superior tampoco tienen un manejo adecuado de los números negativos. Los autores Gallardo y Rojano (1987) confirman que “los números enteros, constituyen uno de los obstáculos más fuertes con que se enfrenta la enseñanza del álgebra”.
Al revisar las investigaciones que se han realizado en esta temática, se encontró que la mayoría de los trabajos están realizados en educación primaria y secundaria, algunos en educación superior.
Para entender esta problemática, esta investigación se pregunta:
¿Cuáles son las dificultades más frecuentes que se aprecian durante el aprendizaje de los números enteros y éstas son susceptibles de disminuirse con la implementación de un cuadernillo de ejercicios especiales, en estudiantes de una preparatoria pública?
Objetivo general: Identificar las dificultades más frecuentes que se aprecian durante el aprendizaje de los números enteros y determinar si éstas son susceptibles de disminuirse con la implementación de un cuadernillo de ejercicios especiales, en estudiantes de la Preparatoria Oficial 222.
Marco Teórico: Modelos Teóricos locales
Los Modelos Teóricos Locales (MTL), constituyen un marco teórico y metodológico “…para la investigación en matemática educativa porque…” permite analizar a profundidad las dificultades que se producen en el aula. (Rodríguez, Filloy y Gómez, 2020, p. 60). La observación es la herramienta metodológica, para comprender los procesos cognitivos que se articulan en la competencia formal y pragmática (Filloy, Rojano y Puig, 2008). La ruta metodológica se estructuró considerando los componentes de los MTL: Competencia Formal, Competencia Cognitiva, Competencia de Comunicación y la Competencia de Enseñanza.
MTL para la enseñanza y aprendizaje de las matemáticas de los números enteros
Este MTL se ha diseñado para comprender y explicar el problema de la falta de dominio de las operaciones de números enteros en el nivel medio superior de educación, es un problema que influye en el rezago matemático en los estudiantes para acceder a las siguientes áreas de matemáticas, entre ellos el paso de la aritmética al álgebra. Por lo que el interés de esta investigación fue el diseñar acciones para apoyar a los estudiantes.
Componente Formal: Números Enteros
Esta componente tiene como base la conceptualización matemática de los números enteros, por lo que es necesario partir de qué son los números enteros. Para ello, se encontró que durante los siglos VI Y VII:
…los hindúes fueron los pioneros en usar las cantidades negativas como un medio para representar las deudas. No obstante, su uso en esos siglos, la aceptación del concepto de número negativo en Occidente fue un proceso lento, por varios siglos, los números negativos no fueron considerados como cantidades verdaderas, debido a la imposibilidad de representarlos en el mundo físico. En el siglo XIX aún existía entre los matemáticos de occidente una gran desconfianza en el manejo de las cantidades matemáticas. (Aguilar, Bravo, Gallegos, Cerón, y Reyes, 2009).
En la actualidad, la conceptualización de los números enteros se ha consolidado, Maldonado (2010, p. 7) clasifica los números enteros como:
- Números enteros positivos: Se llaman así a todos los números que representen una cantidad. Los números naturales son los enteros positivos, anteponiendo a la representación los enteros positivos el signo (+).
- Números enteros negativos: Los enteros negativos representan una cantidad en contra o algo que no se tiene, se representa anteponiendo el signo (-).
Los “sentidos de uso” de los números negativos se deben a Gallardo, Santos y Hernández (2010):
- Número sustractivo. – La noción de número se subordina a la magnitud. En la resta de dos cantidades a – b, siempre b será menor que a, donde a,b son números naturales, el signo menos solamente tiene un carácter binario a nivel de la operación de sustracción.
- Número signado. Es el número natural al que se le asigna un signo más o un signo menos. Surge la dualidad del signo: binario (signo de la operación de adición o sustracción) y unario (signo asociado al número natural).
- Número relativo. Cuando se concibe la idea de opuestos, en situaciones discretas, así como la idea de simetría en situaciones continuas.
- Número aislado. Cuando se acepta un número negativo como resultado de una operación o solución de un problema o ecuación (p. 306).
Estos referentes matemáticos constituyen el eje de análisis de la investigación.
Componente Cognitiva: Aprendizaje significativo
La introducción a los números enteros comienza en los últimos grados de educación primaria y se consolida durante la educación secundaria; por lo que se espera que, en el nivel de bachillerato, sea una base conceptual para los siguientes niveles de concreción matemática. Sin embargo, para consolidar un pensamiento matemático abstracto superior es necesario desarrollar y promover el aprendizaje significativo de conceptos y representaciones (Ausubel, Novak y y Hanesian (1998). En esta componente se identifican las dificultades que tienen los estudiantes para comprender y conceptualizar a los números enteros y poder acceder a siguientes niveles de pensamiento matemático.
Componente de comunicación. Dificultades para generalizar el contenido matemático
La abstracción matemática se consolida a través del carácter generalizado de la acción (Talizina, 2001), lo que permite la comunicación y junto con la lectura y la escritura, constituyen aprendizajes fundamentales de la educación (Corral, et. al. 2018). Sin embargo, los bajos resultados del aprendizaje de matemáticas, en todos los niveles educación, es que en esta componente se centra en identificar, entender y atender las Dificultades de Aprendizaje de la Matemática (DAM) asociadas a la conceptualización de este contenido matemático.
Fernández (2013) considera factores: a) Insuficientes conocimientos previos, b) Dificultades asociadas a la transición de los naturales a los enteros, c) Dificultades asociadas al desarrollo cognitivo obstaculizando el desarrollo intelectual, la capacidad de razonar y de procesar información. d) Dificultades asociadas a la complejidad matemática, reflejadas en lo operacional y conceptual, como los números negativos. e) Dificultades asociadas a actitudes afectivas hacia las matemáticas: generan bloqueos y repercuten negativamente en el aprendizaje.
Componente de Enseñanza
Esta componente se centra en las acciones que se realizan para promover los procesos didácticos, considerando el aula como el espacio donde se construye una colección de textos, se generan y modelan acciones, que van de lo concreto a lo abstracto, desarrollando gradualmente habilidades matemáticas que les permite a los estudiantes resolver problemas matemáticos. Con estos referentes el diseño de actividades se realiza con base en la componente formal (Filloy, et. al 2008), identificando las necesidades (diagnóstico), secuencias de actividades (Cuadernillos y taller de matemátidcas) y evaluación final (Entrevista Focal). Para Ausubel, et. al. (1998) “la función del profesor es una de las variables más importantes del proceso de aprendizaje” (p. 430). Por lo que es necesario que el docente cuente con una base sólida en el campo cognoscitivo para ser capaz de organizar con claridad la materia de estudio, de explicar lúcida e incisivamente las ideas y de manipular con eficacia las variables importantes que afectan al aprendizaje (Filloy, et. al. 2008).
Metodología de la investigación
Esta investigación es un estudio exploratorio, participaron 76 estudiantes de primer semestre de EPO 222 y para la entrevista focal se seleccionó una muestra por conveniencia de 20 alumnos.
Se estructuró en tres etapas:
- Diagnóstico. – Diseño de un Cuestionario: identificar los conocimientos previos sobre números enteros.
- Desarrollo. – Cuadernillo de Actividades de números enteros: atender las necesidades detectadas en el diagnóstico, se trabajó en sesiones híbridas: presenciales en los talleres de matemáticas y sesiones sincrónicas en línea. Cuestionario de Seguimiento: se aumenta el grado de dificultad y se agregan reactivos de resolución de problemas. Entrevista focal: Proceso de evaluación del trabajo realizado en cada etapa.
- Cierre: Análisis de resultados y Conclusiones
Todos los instrumentos fueron validados por tres expertos en investigación en matemática educativa.
Análisis de Resultados
Cuestionario diagnóstico
El 75% de los alumnos no pudieron resolver operaciones con números signados con signo unario, (Figura 1), los errores de los alumnos se caracterizan por tratar de aplicar las reglas de la multiplicación para operar cantidades de diferente signo. Lo que también es una dificultad para transitar del sistema de números naturales a los números enteros.
Figura 1. Presencia de dificultades al resolver operaciones con números signados con signo unario

El 72% de los alumnos tuvo dificultades para resolver operaciones aditivas con números signados con signo binario (Figura 2), cuando la suma de números negativos se representa con paréntesis. Esta dificultad está asociada a la complejidad de tipo operacional y conceptual para operar con números negativos en operaciones aditivas simples, con diferentes representaciones.
Figura 2. Operación con número signado con signo unario y binario.
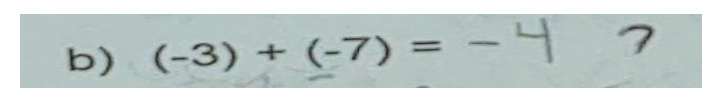
Este fenómeno incrementó su dificultad en la resolución de operaciones multiplicativas, con diferente signo, donde el 75% mostraron dificultades para realizar multiplicaciones y divisiones con números con diferente signo, el 82% no pudo resolver operaciones con números positivos y negativos con potencias positivas.
Cuadernillo de actividades
El cuadernillo de actividades fue entregado a los 76 alumnos de 1°6 y 1°5 a los cuales se les impartió la materia de Matemáticas I y Taller de Matemáticas I, se les entregó en impresiones engargoladas y de manera física. Fueron trabajadas dentro del horario de clases de lunes a viernes en el periodo de agosto – septiembre del 2022, trabajando 30 horas – clase.
La mayoría de los estudiantes que trabajaron el cuadernillo de actividades, entregaron en tiempo y forma las actividades. Todos los alumnos obtuvieron calificaciones aprobatorias en el primer parcial, en las asignaturas de Matemáticas I y Taller de Matemáticas I, en donde, los estudiantes, no solo autoevaluaron los conocimientos, sino que también tomaron en cuenta las actitudes y habilidades Matemáticas. Además de considerar actividades planeadas en la academia de Matemáticas y actividades de ejercicios de nivelación.
La mayor parte de las actividades las contestaron correctamente. Pero al final de la clase, se contestaban los ejercicios, con la finalidad de retroalimentar los ejercicios en donde hubo dificultades.
Con la finalidad de analizar de nuevo, si había dificultades en la solución de las operaciones con números enteros, los alumnos resolvieron un cuestionario de seguimiento.
Cuestionario de seguimiento
En esta etapa, el 41% de los alumnos pudo resolver operaciones con números signados con signo unario, lo que implicó un avance del 16% en su comprensión; sin embargo, siguen presentando dificultades para sumar números negativos, por ejemplo este estudiante hace una resta, acomodando los números 13 – 6 (Figura 3).
Figura 3. Operación con números signados con signo unario

El que las operaciones estén representadas con paréntesis, siguió siendo una dificultad recurrente; como en el siguiente ejemplo (ver figura 4) al encontrarse un signo negativo en medio de los números, el estudiante realiza una resta, sin considerar es una resta entre positivos y negativos, dando como resultado 3 en lugar de 17.
Figura 4. Dificultad al resolver operaciones con números signados con signo binario
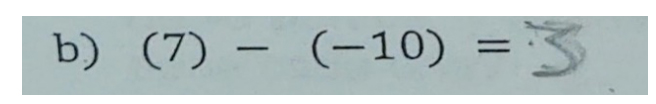
En donde más se apreció el avance fue en reactivos de números signados con signo unario, del 75% se redujo a 59% de respuestas incorrectas; sin embargo, las carencias conceptuales básicas siguen dificultando su comprensión en más de la mitad de los alumnos. Para tratar de entender estos resultados, se realizó un análisis cualitativo de las dificultades que continúan presentándose. De acuerdo con Riviere (citado por Fernández, 2009) se encontró que las dificultades están asociadas a la carencia de conocimientos previos, dificultades de atención y memoria, dificultades asociadas a la complejidad de los objetos matemáticos que son de tipo operacional o conceptual, así como, la dificultad para dar sentido a las cantidades aisladas.
Análisis de la Entrevista Focal
Este espacio se constituyó como proceso de reflexión y análisis por parte de los participantes, el 85% expresó que la asignatura de matemáticas les causa miedo, angustia; mientras que el 15% lo consideran interesante y esencial en su vida cotidiana. Todos los alumnos entrevistados consideraron que su aprendizaje fue más significativo durante las clases presenciales, debido a que los maestros explican y resuelven sus dudas en el momento. El 45%, comentaron que con las tareas virtuales no fueron de mucha utilidad, pues la mayoría de las respuestas ya están en la web, por lo que no hubo aprendizaje.
Consideraron que el Cuadernillo de Actividades fue útil y práctico, dado que sus actividades fueron atractivas, distintas e interesantes, enriquecidas con ejemplos y las explicaciones de la docente les permitió entender y aprender con mayor facilidad. [MR1]
Aunque la mayoría de los estudiantes entregaron en tiempo y forma las actividades del cuadernillo, al responder el cuestionario diagnóstico y cuestionario de seguimiento los resultados no fueron los esperados, se pudo ver que el porcentaje aumentó en el cuestionario de seguimiento al resolver operaciones de números enteros con signo unario, ya que mientras en el cuestionario diagnóstico se obtuvo un 25% de respuestas correctas, en el cuestionario de seguimiento fue un 41%. En la resolución de multiplicaciones hubo de igual forma un aumento del 5% en las respuestas que contestaron correctamente.
Al hacer uso de un cuadernillo de actividades utilizadas el proceso de aprendizaje de los estudiantes fue favorable, ya que, se logró el aumento en el número de respuestas correctas en los temas de operaciones con signo unario y en las multiplicaciones con números enteros.
Después de trabajar el cuadernillo de actividades, se resolvió un cuestionario de seguimiento que permitió visualizar que las DAM seguían presentes. Además de considerar lo señalado por los estudiantes en las entrevistas focales, en donde sugieren hacer modificaciones en el cuadernillo que les permitan disminuir estas dificultades. Lo anterior permitirá en un futuro realizar un análisis y rediseño de las actividades propuestas con la finalidad de disminuir el rezago en las dificultades encontradas.
La mayoría de los entrevistados expresó que las dificultades para resolver los reactivos de los cuestionarios de diagnóstico y de seguimiento, se debieron a que trataban de recordar los procesos de resolución que hicieron en el cuadernillo o cómo lo hacían en las clases presenciales: pero se dieron cuenta de que no era sólo un ejercicio de repetición; por lo que los nervios y la presión los vencieron. De acuerdo con Riviere (citado por Fernández, 2009) éstas son dificultades de tipo afectivo. Para otros alumnos consideraron que sus dificultades están relacionadas con la falta de estudio: “Los procedimientos que seguí, fueron totalmente de los números enteros, pero al no estudiar yo, y, no tener ese compromiso, se me dificultó y no pude hacerlos de la manera correcta”. Otro alumno agregó: “Pues, me confundí mucho, cuáles eran los números positivos y negativos, en varios temas no le llegue a entender porque, aunque el problema estaba bien explicado, yo realmente no llegaba a comprender bien el tema y fue lo que más se me dificultó, porque no recordaba bien lo que acabábamos de ver.” Esta reflexión nos permite comprender que las dificultades también están asociadas a la complejidad de los objetos matemáticos (Fernández, 2013).
[MR1]Es importante comentar que tiene que describir el cuadernillo, en que consiste y si solo se lo dio al alumno y se esperó a que él alumno lo resolviera, o ¿comó fue el proceso de entregar el cuadernillo y como este hizo “magia”?
Conclusiones
El confinamiento por el COVID – 19, provocó crisis mundial, agravando las dificultades de aprendizaje en todas las áreas del conocimiento. En la EPO 222, institución de EMS, se observó que el aprendizaje significativo de los números enteros en los alumnos de primer semestre enfrenta DAM relacionadas con insuficientes conocimientos previos; lo que les dificultó darle sentido a las cantidades negativas aisladas, resolución de operaciones con signos binarios, operaciones binarias con exponente.
Las DAM que se identificaron en los procesos de aprendizaje, son obstáculos cognitivos, que impiden a los alumnos consolidar conocimientos y habilidades fundamentales para ir construyendo las bases conceptuales de los semestres posteriores: Álgebra, Trigonometría, Geometría y Calculo Diferencial e Integral.
La entrevista focal fue un espacio que permitió que los estudiantes participar de un proceso de evaluación, con la oportunidad de expresar y de reflexionar sobre las dificultades a las que se enfrentaron, para comprender el contenido de los números enteros.
A la profesora – investigadora le posibilitó promover un proceso de introspección para que los estudiantes pudieran analizar los resultados obtenidos en el cuestionario diagnóstico y de seguimiento; revisar la funcionalidad y pertinencia del cuadernillo de actividades; así como la importancia de poner atención a las necesidades de tipo afectivo; debido que éstas últimas no fueron consideradas para analizar las DAM en esta investigación.
Los MTL permitieron estructurar una ruta metodológica para llevar a cabo la presente investigación, a partir de sus cuatro componentes de competencia: Formal, cognitiva, de comunicación y de Enseñanza. Centrando el énfasis en lo formal (matemático) y lo cognitivo, bajo el enfoque de aprendizaje significativo de Ausubel.
Los instrumentos diseñados permitieron estructurar el trabajo en tres momentos:
- Diagnóstico: para conocer las necesidades de los alumnos
- Desarrollo: a través del cuadernillo de actividades y el cuestionario de seguimiento, para valorar los avances y dificultades.
El avance en los aprendizajes fue mínimo, a pesar de las actividades que se implementaron con el cuadernillo de actividades durante las clases normales y el taller de matemáticas, al principio en sesiones en línea y después de forma presencial, las dificultades de aprendizaje matemático (DAM) se vuelven a presentar, en temas como: leyes de signos con números enteros, leyes de exponentes con números enteros, jerarquía de operaciones.
- Cierre: La participación del 26.31% de alumnos de cada grupo, en la entrevista focal, permitió identificar el componente afectivo, como un factor que dificulta el aprendizaje en matemáticas, por lo que es necesario recuperar una línea de investigación.
Como producto de esta investigación, se considera fundamental:
- Abrir nuevas líneas de investigación para analizar las dificultades de conceptualización de números enteros en la Educación Media Superior, para proponer acciones concretas que posibiliten a los estudiantes de este nivel educativo, superarlas y consolidar las bases matemáticas en aritmética para transitar al álgebra, geometría analítica, trigonometría, cálculo diferencias e integral.
- Abrir líneas de investigación con énfasis en las implicaciones de los factores afectivos en el aprendizaje de Matemáticas en el nivel Medio Superior.
Referencias
Aguilar, A., Bravo, F., Gallegos, H., Ceron, M. y Reyes, R. (2009). Matemáticas Simplificadas. Prentice Hall. México. 2da, edición.
Ausubel, D, Novak, J. y Hanesian, H. (1998). Psicología Educativa, un punto de vista cognitivo. Ed. Trillas. México. Décimo tercera reimpresión.
Corral, I. Castro, R. y Corral, Y. (2018). Dificultades de aprendizaje de la matemática: cómo ayudar al estudiante. Biblioteca Digital, Vol. 12 No. 23. http://bdigital2.ula.ve:8080/xmlui/handle/654321/4140
Fernández, A. (2013). Dificultades y errores en el aprendizaje de las Matemáticas en ESO y Bachillerato. https://reunir.unir.net/bitstream/handle/123456789/1808/2013_04_09_TFM_ESTUDIO_DEL_TRABAJO.pdf?sequence=1&isAllowed=y
Filloy, E., Rojano T., y Puig L. (2008). Educational Algebra: A Theoretical and Empirical Approach. Nueva York: Springer.
Gallardo, A y Rojano, T. (1987). Áreas de dificultades en la adquisición del lenguaje aritmético. https://www.researchgate.net/profile/Teresa-Ceballos/publication/273722758_AREAS_DE_DIFICULTADES_EN_LA_ADQUISICION_DEL_LENGUAJE_ARITMETICO-ALGEBRAICO/links/5509bc510cf20f127f9073ce/AREAS-DE-DIFICULTADES-EN-LA-ADQUISICION-DEL-LENGUAJE-ARITMETICO-ALGEBRAICO.pdf
Gallardo, A. y Basurto, E. (2010). La negatividad matemática: antesala histórica de los números enteros. Revista Latinoamericana de Investigación en Matemática Educativa. 255-268. https://www.redalyc.org/pdf/335/33558827002.pdf
Gallardo, A., Santos, N. y Hernández, J. (2010). La aparición simultánea de los sentidos de uso de los números negativos y el cero en alumnos de secundaria. Un estudio de caso. En M. M. Moreno, a. Estrada, J. Carrillo, y T. a. Sierra, (Eds.), Investigación en Educación Matemática XIV Simposio SEIEM (pp. 303-314). http://funes.uniandes.edu.co/1697/1/346_2010Laaparicion_SEIEM13.pdf
Hernández, D. y Noriega, J. (2017). La aritmética como base indispensable para el aprendizaje del álgebra. https://revistas.uaq.mx/index.php/padi/article/view/74/660
Hernández, R. y Mendoza, C. (2018). Metodología de la investigación. Las rutas: cuantitativa, cualitativa y mixta. Ed. McGRAW-HILL. México. [PDF].
Hevia, F. y Vergara, S. (2021). Rezago de aprendizajes básicos y brecha digital en el contexto de COVID-19 en México. Perfiles Educativos | vol. XLIV, núm. 176. https://perfileseducativos.unam.mx/iisue_pe/index.php/perfiles/article/view/60478/52939
IMCO (2021). Educación en pandemia: los riesgos de las clases a distancia. Disponible en: https://imco.org.mx/wp-content/uploads/2021/06/20210602_Educacio%CC%81n-en-pandemia_Documento.pdf
Maca, A. (2016). La enseñanza de los números enteros un asunto sin resolver en las aulas. PDF. https://ridum.umanizales.edu.co/xmlui/bitstream/handle/20.500.12746/2640/TRABAJO%20FINAL%20MAESTR%c3%8dA%20LA%20ENSE%c3%91ANZA%20DE%20LOS%20NUMEROS%20ENTEROS%20UN%20ASUNTO%20SIN%20RESOLVER%20EN%20LAS%20AULAS.pdf?sequence=1&isAllowed=y
Maldonado, G. (2010). “Aprendizaje significativo de los números enteros con énfasis en los números negativos”. Tesina de la Universidad Pedagógica Nacional. http://bgtq.ajusco.upn.mx:8080/jspui/bitstream/123456789/423/1/27352.pdf
Rodríguez, M. Filloy, E. Gómez, A. (2022). Dificultades en la construcción de los números naturales incluyendo el cero, con estudiantes de 6 a 8 años. En Revista Enseñanza de las Ciencias, 38-3, pp. 55-80. https://ensciencias.uab.cat/article/view/v38-n3-rodriguez-gomez-filloy
Talizina, N. Comp. (2001). La formación de las Habilidades del Pensamiento Matemático. San Luis Potosí: Universidad Autónoma de San Luis Potosí.